小编：如何在直时时了解统一的加速度参考系统？如何在挫败感的特殊理论中扩大加速经典含义的平等运动？林德勒坐标
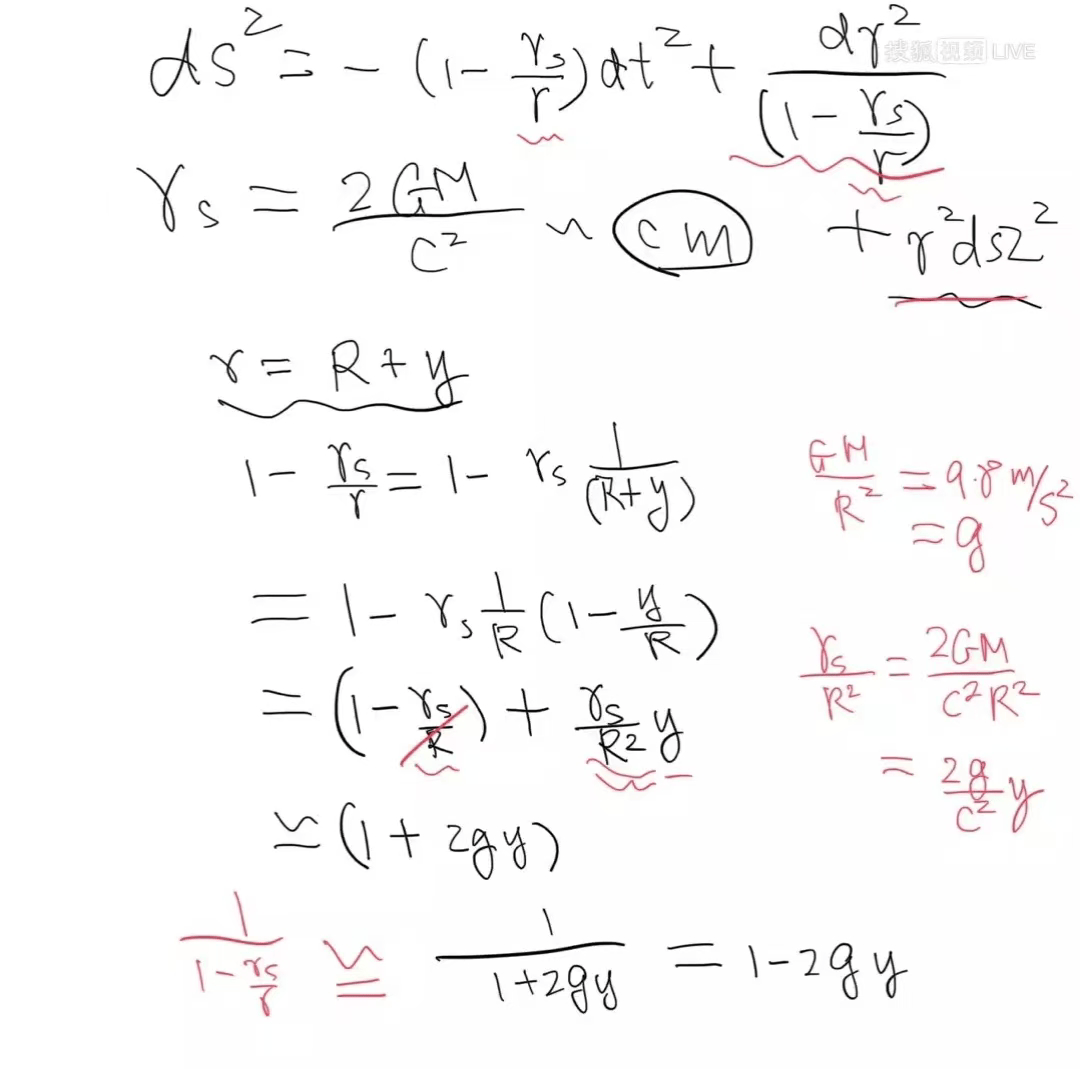如何在直时时了解统一的加速度参考系统？如何在挫败感的特殊理论中扩大加速经典含义的平等运动？林德勒的坐标是如何来自的？ Schwasi建议如何描述地球表面附近加速度的平等运动？时空和schwarzish指标在与Schwarzish度量一致的地面的加速参考系统中看到？他们对大地学的行为相同吗？ 5月25日12:00，启动了“张乔阳的物理课”。 Sohu的创始人，董事长兼首席执行官兼物理博士Zhang Chaoyang在Sohu Video Live Broadcast Room中。他首先检查了Schwarsey的空间和空间，并在地面上展示了他的估计，从而导致了同样加速运动的几何形象。从洛伦兹的转换的角度来看，林德勒坐标是thenderive的，在加速参考中重写了线元素的形式Minh的时空系统。最后，从测量学的角度来看，将加速在地面上加速schwarzish时空的例子与加速林德勒空间中的颗粒进行了比较，从而导致爱因斯坦的深层动机提出了同等的原则。 。但是，在现实生活中存在许多情况，存在非惯性系统。例如，当您乘坐总线和驾驶员到加速器的步骤并开始加速时，您就处于非文字参考系统中。这自然会导致一个问题：在同样加速的非侵入参考系统中，Minh空间有什么样的结构？这个问题吸引了他对爱因斯坦特殊理论爱因斯坦（Einstein）的关注。他分别于1907年和1912年发表了两篇德国论文，并在非静态系统的物理学方面进行了深入思考。这是对非侵入系统的研究，促使爱因斯坦提出了“ E原理的概念质量”并为建立一般事件奠定了基础。林德勒时空是对统一参考系统中观察到的平坦时空的描述形式。我们比较了Rindler时空的线性元素以及Schwarzishi gauges以及schwarzishi gauges，它们描述了地球的引力领域，并在此地区进行了整个地面的构想，该领域是一致的，该领域是一致的，该层面是一致的，该层面是一致的，该领域是一致的。相应的原理：在局部范围内，参考系统的重力和加速度无法清楚地描述这一点。汽车以恒定的速度行驶，这是林E具有惯性参考系统S1，S2，S3 ...，它们的相应速度为V1，V2，V3 ....随着速度的载体继续加速，它将超过车辆的相等速度。但是，在每时每刻，总是有一个恒定的汽车速度，并且汽车加速度相同，并且它们都立即静止。因此，加速运动可能会作为一系列惯性的即时共同动力系统的划分。 i -set到车辆速度本身的坐标时间为τ，x空间的坐标，地面参考系统的坐标为y =（t，x）。 Y的坐标小元素可以写为：展开全文
（Zhang Chaoyang介绍了加速参考系统和惯性参考系统的物理图像）
随着对上课中提到的洛伦兹和伪旋转的转化的了解，我们知道任何V或β速度都可以通过速度θ表示，其中：
在某个妈妈Accelerathis的参考系统的实现就是IT。因为参考系统将自己视为立即静止的，所以DX = 0，并且其所经历的时间等于超速系统本身的原始Dτ时间。目前，洛伦兹的转变表示为：
其中ϕ = - 是与θ不同的负签名的速度，因为从参考框架的速度来看，地面参考框架沿负方向移动。这提供了三个之间的关系：
随着时间的流逝，加速度的同等移动意味着对象的速度在不断变化，相应的速度ϕ不再是平行的，而是随着时间的推移出现的函数。它反映了非电力运动的重要特性。
在当前系统中，我们拥有的唯一参数是加速。但是，引入加速理论ISA问题是多么合理的我们需要解决的问题。换句话说，我们需要思考：如何自然概括“统一Accelera的概念ted movement" in Newtonian mechanics in the framework of special frustration? As such, let's first examine a more familiar classic example - a constant circumferential motion in the two -euclidian two -DECLIDIAN space. In Newtonian mechanics, if a grain moves at a constant speed along with the circumference and its position vector is marked as R, then the tangential micronumeral DR is a first-order tenor, which means the geometric object itself remains unchanged在各种坐标系统下，其组件集成了坐标系统。
其中矢量的最后一个方向是指向圆心中心的单位向量，并且速度大小由角速度产物ω和半径r：
因为速度在恒定旋转过程中保持不变，所以加速度的大小（或mOdulus Square）也是一个类似的广场：
（张乔阳在欧几里得空间中引入了旋转）
在特殊挫败感中，我们将上述旋转状况扩展到“伪旋转”情况下的循环速度。由于本质，这两个是扭曲的，但是时间和空间的几何背景是不同的。在伪旋转的情况下，粒子以速度ϕ移动，其四个维速度为：
相应的四维加速度为：
我们计算四维加速度的模量
这些笨蛋，g这是Minshi的时空规则
（张·乔阳（Zhang Chaoyang
该结果表明，四维加速度的模量的平方和原始时间的速度变化速率的平方完全相等。类似于牛顿力学的情况速度速度与循环运动速度一致，我们还希望达到相等的超速参考系统系统的四维加速度模式是一致的。因此，如果速度设置为α，
从这里
我们采取了整体pare -same零的位置。将此结果替换为Lorentz转换的先前表达式，您可以得到：
包括上述两个方程式，并使整体pare -smeThat Zero零，并获得：
因此，世界线方程得出：
它表明，在土地参考系统中，均匀速度系统中固定点的世界线是一条双曲线线，并且从X轴到源到源的相交点的距离为1/α。这种双曲线形状是相等运动的几何特征，它反映了“伪旋转”性质。
（张乔阳引入了林德勒时空的几何特征）
Rindler时空和测量分析
完成e Rindler坐标系，我们希望不仅描述了某个加速度的双曲线路径，而且还占据了整个Rindler区域（这里是指在Minh时空的正确位置）。到目前为止，我们引入了一个新的空间坐标X，以识别不同速度的双层线线。在上面，我们使世界有一个相等的加速度差异：
相应的双曲线是：
如果我们用连续变量X替换双曲线的“距离” 1/α并维持加速α到双曲线函数，那么我们可以参数该家族的双曲线到坐标系。目前，让参考系统的原始时间τ更改为坐标t，并获得了促销形式：
此调整意味着每个固定X对应于同样加速的观察者。不同的加速轨迹对应于不同的X值，双曲线线填充了Minh空间的正确位置。作为sho上图中的wn。
我们可以概括坐标衍生物的整个元素的转换，因此时空的比例写在统一的加速度参考系统下（即Rindler坐标系）。会改变
在Minshi时空牢固地元素
得到
这是Rindler坐标下的Minh-Shire太空线的元素。可以看出，时间方向的系数度量不再是常数，而是依靠空间坐标X的操作。这是我们第一次遇到相对改变位置系数系数的特殊理论。
为了促进对加速和空间坐标之间关系的理解，我们进一步进行协调变化：
那里
用线的元素替换并获得：
接下来，我们将将光常量C的速度恢复到国际单位系统，从而
在这个蒂姆e，KWE将加速α作为地面上的重力加速度αα= g = 9.8 m/s^2，并且y的协议
所以
这意味着在时间部分之前的比例系数非常接近-1，我们可以进行泰勒的扩展以获取近似线元素：
（张乔阳在远处共享时间的线性元素和林德勒空间）
然后在林德勒的时空中研究大地学。大地的方程是：
如果限制不相关，则晶粒速度小于光速，因此可以大致：
因此，加速三维空间表示为：
由于粒子仅沿y方向移动，因此只需要考虑高棉符号的100个部分，即：
该结果表明，在林德勒时空中，y方向中psarticle的速度始终是α，这与我们引入的加速度定义完全相同。值得注意的是，转型
继续项1/α，令状国际单位体系中的十个：
这意味着与加速度的世界线为α，其与x = 0的距离主要促成第一项c^α，其数量级为10^16米（α= 9.8 m/s^2），而y的产率仅为1米。因此，可以认为，这种加速度是从远距离距离α强度形成的加速度的同等运动。
由Schsassi在表面上测量产生的加速度和等效原理
让我们回顾一下Schwarsey空间线的元素：
Schwarzsi的半径是
和重力的质量。在这里，我们只关心粒子在径向方向上的运动（即R的方向），并且仅考虑地球表面附近的位置，因此我们不会忽略角色的服装并简化了以下位置的元素：
为了评估表面附近的空间和时间结构，我们将径向坐标r写为半径的总和土壤r = 6400公里，距离的部分变化y：
用系数替换
由于地球schwsi的半径仅为3mm，而土壤的半径为r = 6400 km，因此两者之间的差异超过六个数量级。因此，对第一项RS/R的持续校正非常小。可以通过重新定义时间和径向坐标来获得它，然后保留在Y的线性项中以获得：
记住更多：
在
它是表面上的重力加速度。因此，该行的元素可以写为：
目前，一部分量表ISNEXT，我们回顾了颗粒的测地运动。在低速下，四个维速度和四个维度加速度大约是
因此，加速三维空间表示为：
由于颗粒仅在径向方向移动，因此只有Y物质仍然存在：
克里符号的表达是：
我们不关注2gy最后一步是因为数量级为10^-16，与前1个相比，这可能会忽略。这导致y方向加速为
上面的表达表明加速是地面加速度加速的相反方向，代表续集，因此我们重新定义了牛顿通用引力的末端。在地球产生的schwarzish时空区域附近的区域中，线元素大约是一个静态统一的速度固定场，其速度与牛顿经典重力提供的结果一致。这表明地面附近的重力场可以被视为等效加速参考系统。但是该结果来自几何视图的纯点，这不是在粒子中“释放”的力，而是弯曲时空中的大地测量表现。
（张·乔阳（Zhang Chaoyang）在地球上分享地球学）
我们计算两个DI中粒子的加速度情况下：一个是林德时空，加速α自然源自超速参考系统；其余的是通过在地球表面附近的schwarzish时空的尺寸扩展获得的G速度。当我们服用时
目前，加速的参考系统是您完全是本地引力场结构的结构，无法理解它们的地球行为。换句话说，如果观察者处于同样加速的非电力系统或同等的引力领域，则无法通过物理实验来判断他们。
这正是爱因斯坦等效原理的表达：在一个时间和空间，引力效应等于非电力运动。这一原则不仅揭示了惯性和重力的力量之间的密切联系，而且还为建立一般亲戚提供了一个理论的起点。但是，应该强调等效原则的应用范围仅限于“本地”。当制定较大范围内的空间结构时，出现曲率效应（水力），可以揭示引力场的几何特性，从而使我们能够识别加速度的几何资源是几何（真正的引力弯曲）还是运动学（加速度参考系统）。
据了解，周日中午12点在SOHU视频中现场直播“张乔阳班”。网民可以搜索“ Zhang Chaoyang”来“遵循Sohu视频应用程序的流”，以观看实时广播和过去时代的完整视频重播；请按照“张Chaoyang”物理课程帐户查看“知识”点数简短的视频；此外，您还可以在SOHU新闻应用程序的“ SOHU技术”帐户中阅读每个物理课程的详细文章。回到Sohu看看更多
当前网址：https://www.ajitaro.com//a/keji/621.html
